그래프를 탐색하는 방법에는 크게 깊이 우선 탐색(DFS)과 너비 우선 탐색(BFS)이 있다.
그래프란, 정점(node)과 그 정점을 연결하는 간선(edge)으로 이루어진 자료구조의 일종을 말하며, 그래프를 탐색한다는 것은 하나의 정점으로부터 시작하여 차례대로 모든 정점들을 한 번씩 방문하는 것을 말한다.
1. 깊이 우선 탐색 (DFS, Depth-First Search)
: 최대한 깊이 내려간 뒤, 더이상 깊이 갈 곳이 없을 경우 옆으로 이동
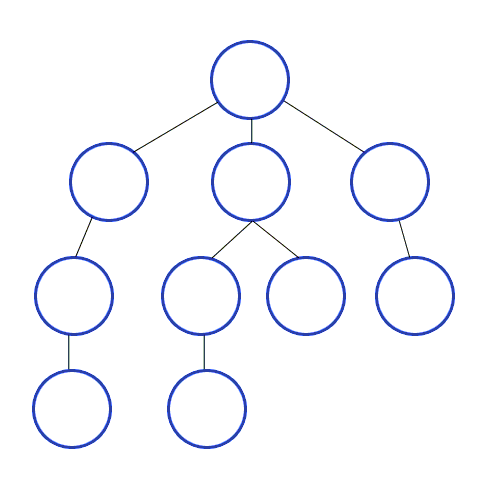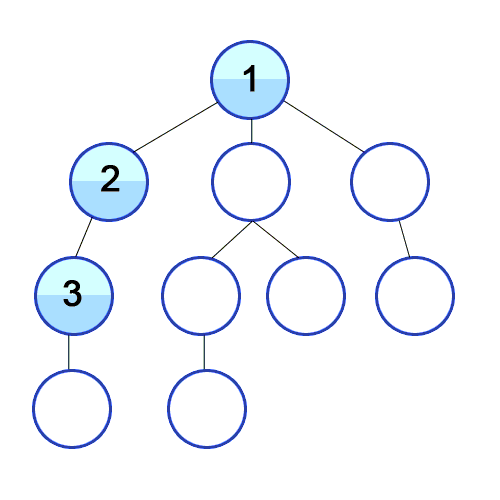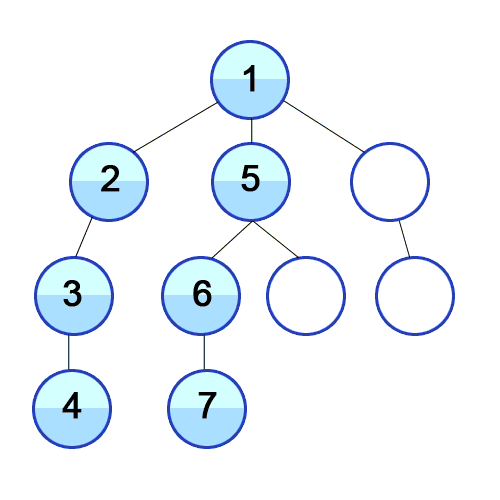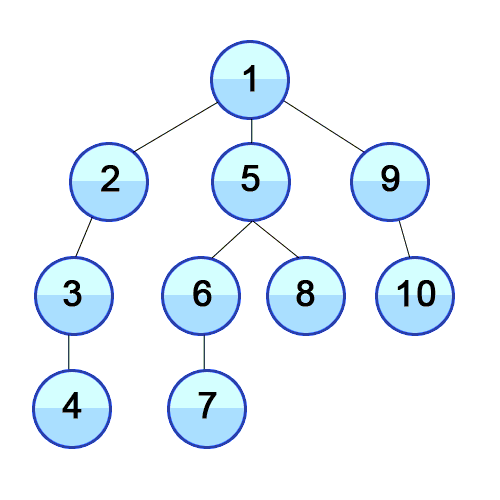
💡 깊이 우선 탐색의 개념
루트 노드(혹은 다른 임의의 노드)에서 시작해서 다음 분기(branch)로 넘어가기 전에
해당 분기를 완벽하게 탐색하는 방식을 말한다.
예를 들어, 미로찾기를 할 때 최대한 한 방향으로 갈 수 있을 때까지 쭉 가다가
더 이상 갈 수 없게 되면 다시 가장 가까운 갈림길로 돌아와서 그 갈림길부터 다시 다른 방향으로 탐색을 진행하는 것이 깊이 우선 탐색 방식이라고 할 수 있다.
1. 모든 노드를 방문하고자 하는 경우에 이 방법을 선택함
2. 깊이 우선 탐색(DFS)이 너비 우선 탐색(BFS)보다 좀 더 간단함
3. 검색 속도 자체는 너비 우선 탐색(BFS)에 비해서 느림
2. 너비 우선 탐색 (BFS, Breadth-First Search)
: 최대한 넓게 이동한 다음, 더 이상 갈 수 없을 때 아래로 이동
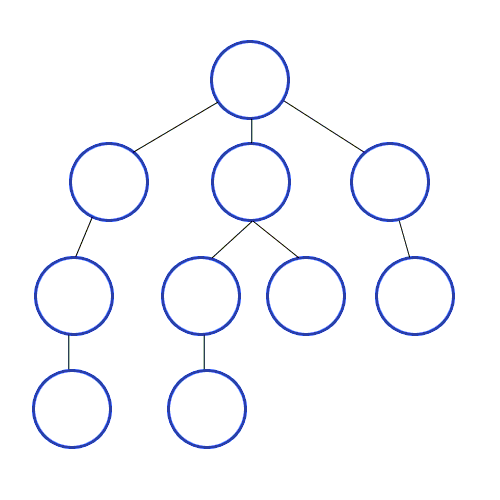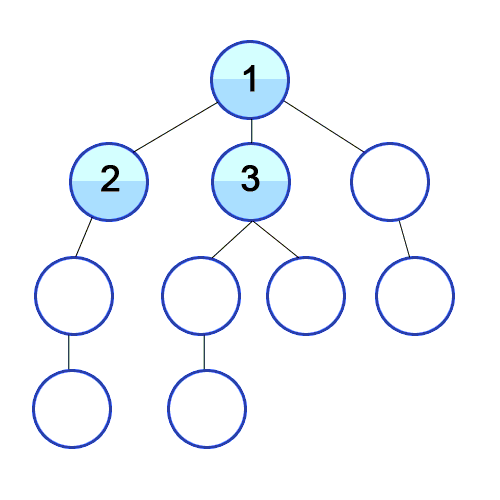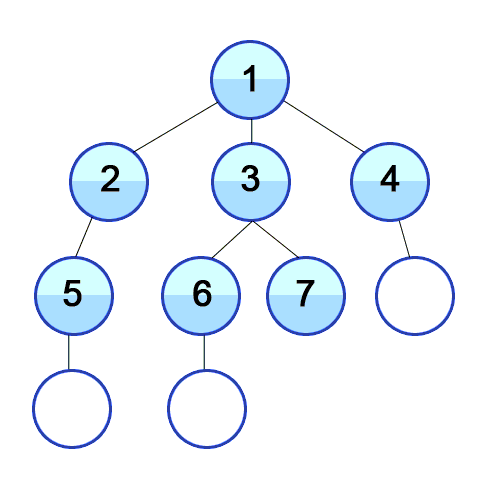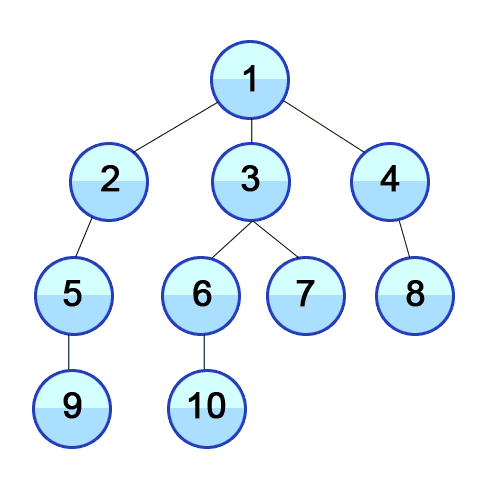
💡 너비 우선 탐색의 개념
루트 노드(혹은 다른 임의의 노드)에서 시작해서 인접한 노드를 먼저 탐색하는 방법으로,
시작 정점으로부터 가까운 정점을 먼저 방문하고 멀리 떨어져 있는 정점을 나중에 방문하는 순회 방법입니다.
주로 두 노드 사이의 최단 경로를 찾고 싶을 때 이 방법을 선택합니다.
ex) 지구 상에 존재하는 모든 친구 관계를 그래프로 표현한 후 Sam과 Eddie사이에 존재하는 경로를 찾는 경우
- 깊이 우선 탐색의 경우 - 모든 친구 관계를 다 살펴봐야 할지도 모름
- 너비 우선 탐색의 경우 - Sam과 가까운 관계부터 탐색
3. 깊이 우선 탐색(DFS) 과 너비 우선 탐색(BFS) 비교
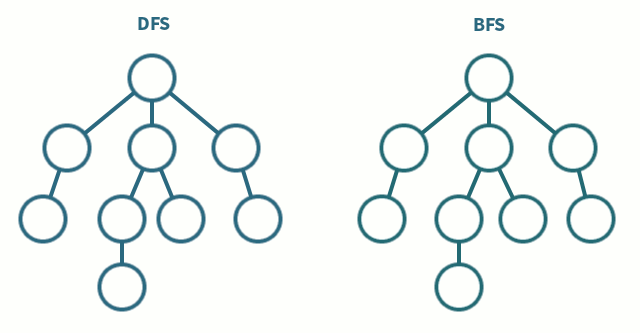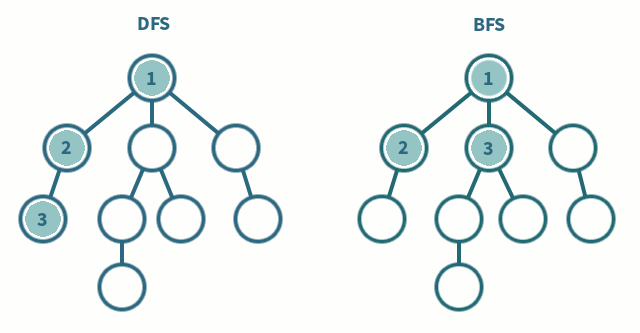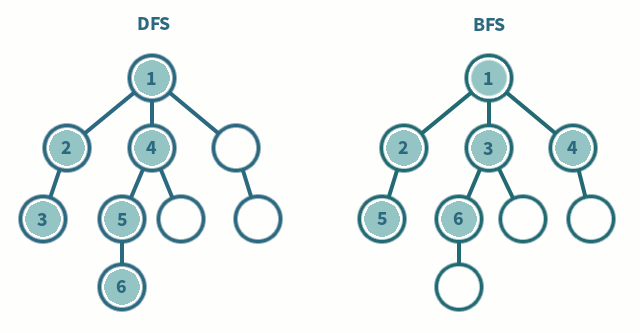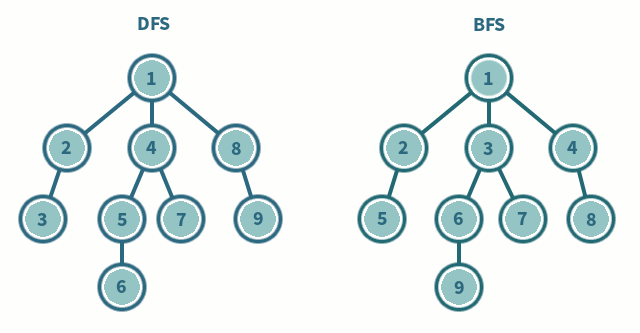
| DFS | BFS |
| 현재 정점에서 갈 수 있는 점들까지 들어가면서 탐색 | 현재 정점에 연결된 가까운 점들부터 탐색 |
| 스택 또는 재귀함수로 구현 | 큐를 이용해서 구현 |
💡DFS와 BFS의 시간복잡도
두 방식 모두 조건 내의 모든 노드를 검색한다는 점에서 시간 복잡도는 동일합니다.
DFS와 BFS 둘 다 다음 노드가 방문하였는지를 확인하는 시간과 각 노드를 방문하는 시간을 합하면 됩니다.
N은 노드, E는 간선일 때
인접 리스트 : O(N+E)
인접 행렬 : O(N^2)
일반적으로 E(간선)의 크기가 N²에 비해 상대적으로 적기 때문에
인접 리스트 방식이 효율적이다.
3. 깊이 우선 탐색(DFS)과 너비 우선 탐색(BFS) 활용한 문제 유형/응용
DFS, BFS은 특징에 따라 사용에 더 적합한 문제 유형들이 있습니다.
1) 그래프의 모든 정점을 방문하는 것이 주요한 문제
단순히 모든 정점을 방문하는 것이 중요한 문제의 경우 DFS, BFS 두 가지 방법 중 어느 것을 사용하셔도 상관없습니다.
둘 중 편한 것을 사용하시면 됩니다.
2) 경로의 특징을 저장해둬야 하는 문제
예를 들면 각 정점에 숫자가 적혀있고 a부터 b까지 가는 경로를 구하는데 경로에 같은 숫자가 있으면 안 된다는 문제 등, 각각의 경로마다 특징을 저장해둬야 할 때는 DFS를 사용합니다. (BFS는 경로의 특징을 가지지 못합니다)
3) 최단거리 구해야 하는 문제
미로 찾기 등 최단 거리를 구해야 할 경우, BFS가 유리합니다.
왜냐하면 깊이 우선 탐색으로 경로를 검색할 경우 처음으로 발견되는 해답이 최단거리가 아닐 수 있지만, 너비 우선 탐색으로 현재 노드에서 가까운 곳부터 찾기 때문에 경로를 탐색 시 먼저 찾아지는 해답이 곧 최단거리기 때문입니다.
이밖에도
- 검색 대상 그래프가 정말 크다면 DFS를 고려
- 검색 대상의 규모가 크지 않고, 검색 시작 지점으로부터 원하는 대상이 별로 멀지 않다면 BFS
4. DFS와 BFS을 사용한 c++코드
DFS 알고리즘에 경우 두 가지 방법으로 풀 수 있는데,
첫 번째로 스택을 이용하는 것
두 번째로 재귀함수를재귀 함수를 이용하는 것인데, 재귀 함수를 이용하는 것이 가장 보편적이고 짧은 코드를 작성할 수 있다.
재귀 함수란 함수 내부에서 함수가 자기 자신을 또다시 호출하는 함수를 의미합니다.
이러한 재귀 호출은 자기가 자신을 계속해서 호출하므로, 끝없이 반복되기 때문에
함수 내에 재귀 호출을 중단하도록 조건이 변경될 명령문을 반드시 포함해야 합니다.
// DFS - Recursion
void dfs_recursion(int x, int y) {
// 함수에 들어왔으면 -> 방문으로 표시
visited[x][y] = true;
// 해당 단지의 집의 수를 증가시킴
groups[group_id]++;
// 해당 위치의 주변을 확인
for(int i = 0; i < 4; i++){
int nx = x + dx[i];
int ny = y + dy[i];
// 지도를 벗어나지 않고
if(0 <= nx && nx < n && 0 <= ny && ny < n){
// 집이면서 방문하지 않았다면 -> 방문
if(map[nx][ny] == 1 && visited[nx][ny] == false){
dfs_recursion(nx, ny);
}
}
}
}BFS 알고리즘은 큐(Queue)를 사용해서 문제를 해결하면 됩니다.
// BFS
void bfs(int x, int y){
queue< pair<int,int> > q; // 이용할 큐, (x,y) -> (행, 열)
q.push(make_pair(x,y)); // pair를 만들어서 queue에 넣습니다.
// 처음 x,y를 방문 했기때문에
visited[x][y] = true;
groups[group_id]++;
while(!q.empty()){
// 큐의 현재 원소를 꺼내기
x = q.front().first;
y = q.front().second;
q.pop();
// 해당 위치의 주변을 확인
for(int i = 0; i < 4; i++){
int nx = x + dx[i];
int ny = y + dy[i];
// 지도를 벗어나지 않고
if(0 <= nx && nx < n && 0 <= ny && ny < n){
// 집이면서 방문하지 않았다면 -> 방문
if(map[nx][ny] == 1 && visited[nx][ny] == false){
visited[nx][ny]=true;
// 해당 단지의 집의 수를 증가시킴
groups[group_id]++;
// 큐에 현재 nx,ny를 추가
q.push(make_pair(nx,ny));
}
}
}
}
}
참고링크
인접 행렬 : O(N²)
'책장 > 알고리즘' 카테고리의 다른 글
| [프로그래머스]타겟넘버 (0) | 2021.04.30 |
|---|---|
| 완전탐색 (0) | 2021.04.24 |
| 힙 (0) | 2021.04.23 |
| 해시 (0) | 2021.04.23 |

